Measures of Central Tendency
Central tendency stands for summary values in the data. It represents the central value for the whole dataset. It provides a single value instead of multiple values that are helpful to understand the system. For example, the average monthly sale is a good indicator of sales for any product.
Let’s discuss the following central tendency measures.
- Mean: Mean or arithmetic average is the ratio of the sum of observations to the total number of observations. for example, the mean of 6, 3, and 9 is (6+3+9)/3 = 18/3 = 6
- Median: Median is the middle value of the entire data. It divides the whole data into two parts. It is also called as 50th percentile. The median value will not be affected by outliers because it is the “middle” value of all data points. For example, the median of 6, 3, and 9. The ascending order of values is (3, 6, 9). 6 is the middle value.
- Mode: Mode is the highest frequency value in the entire data set. Data can have more than one mode such as Uni-modal, Bi-modal, and Multi-modal. For example, The mode of {1,2,2,1,1,3,1,2,4,4} is 1 because it occurred maximum times(4 times) in the given list.
Here are some key points about central tendency measures:
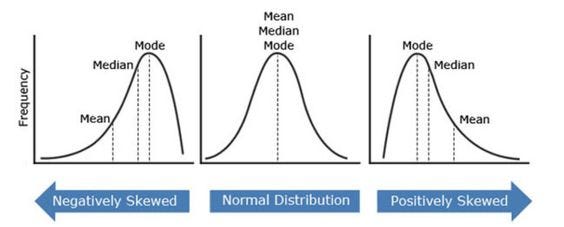
- Outliers will affect only the mean value of the data and less affect the median or mode value of data.
- The median value is useful for skewed data such as income data.
- The mean value is useful for symmetric data because, in the case of skewed data, it gets influence by outliers.
- If the mean=median=mode then we can say that the data is symmetrically distributed about the mean. So the greater the difference among these measures the more asymmetrical the data.
Geometric and Harmonic Mean
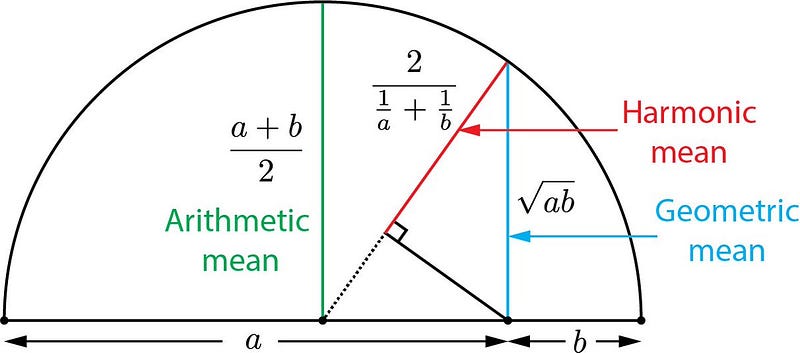
The harmonic mean is the reciprocal of the arithmetic mean of reciprocals. Average speed and flow of liquid are examples of harmonic mean.
The geometric mean multiplies the numbers together and then takes a square root. It offers a good application where units of the indicator are different. Compound interest from year to year is an example of a geometric mean.
Geometric View of different type of mean
Let’s see a very interesting relationship between arithmetic, geometric, and harmonic mean using geometry:
We can easily conclude here AM>GM>HM.
Let’s see a summary table for all the central tendency measure.
Summary
Central tendency measures are very important metrics for exploratory data analysis. It has the capability to summarize the set of observations around a central value. In summary, we can say that mean is an average value median is the center value, and mode is the most frequent value in the set of observations.