Solving Cargo Loading Problem using Integer Programming in Python

Learn how to use Python PuLP to solve Cargo loading problems and Knapsack Problems using Integer Programming.

Linear programming deals with non-integer solutions but in certain scenarios, we need integer solutions such as the number of products to manufacture, number of apartments to construct, number of trees to plan. In this approach, we optimize the linear function and set of linear constraints on integer variables. Integer programming is widely utilized in the area of job scheduling, inventory management, transportation, computer science, and production planning.

In this tutorial, we are going to cover the following topics:

Types of Integer Programming

There are three types of Integer programming problems:

1. Pure Integer Problems: In this type of problem, all the variables have integer solution.
2. Mixed Integer Problems: In this type of problem, some of the variables have integer and some of the variable have the continuous solution.
3. 0-1 Integer Problems: In this type of problem, all the varaibles requires value of 0 or 1.

Knapsack Problem

The knapsack problem is defined as how many units of each different kind of item or product to put in a knapsack with a given capacity in order to maximize profit. It is also known as the fly-away kit problem because a jet pilot decides the most valuable items to take abroad a jet. The knapsack problem is a special case of integer programming where the objective function is maximized with a single less than or equal to linear constraint. It has many applications in the real world.

Cargo Loading Problem

The cargo loading problem is a typical example of a knapsack problem. This type of problem solves the capacity planning problem of a shipment. We load the items into a shipment with limited capacity. The main objective is to load the most optimum items in the shipment.

Suppose there are n items 1,2,3 … n and the number of units of each item is m_i. The weight per unit of item i is w_i, r_i is the revenue per unit of item I, and W is the total capacity of cargo.

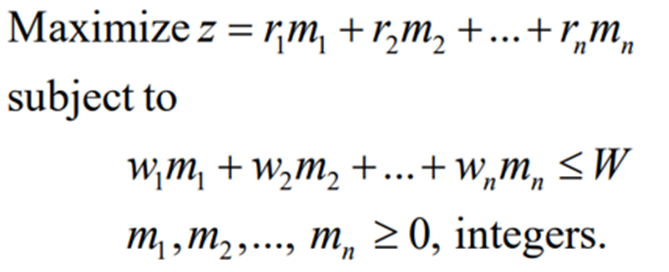
Understand the problem

One Cargo shipment of Shakti Pumps has a capacity of 10 tons. Shakti Pumps wants to ship three types of pumps A, B, and C in this shipment.

• A pump weight of 1 ton and profit of $12 (X₁)
• B pump weight of 2 tons and profit of $25 (X₂)
• C pump weight of 3 tons and profit of $38 (X₃)

Objective Function:

Maximize Z = 12X₁ + 25X₂ + 38X₃

Constraints:

12X₁ + 25X₂ + 38X₃ ≤ 10 (Cargo storage capacity 10 ton)

Initialize LP Model

In this step, we will import all the classes and functions of pulp module and create a Maximization LP problem using LpProblem class.

# Import all classes of PuLP module
from pulp import *

# Create the problem variable to contain the problem data
model = LpProblem("Cargo-Loading-Problem", LpMaximize)

Define Decision Variable

In this step, we will define the decision variables. In our problem, we have three variables A, B, and C. Let’s create them using LpVariable class. LpVariable will take the following four values:

• First, arbitrary name of what this variable represents.
• Second is the lower bound on this variable.
• Third is the upper bound.
• Fourth is essentially the type of data (discrete or continuous). The options for the fourth parameter are LpContinuous or LpInteger.

# Define Decision Variables
x1 = LpVariable("A", 0, None, LpInteger)
x2 = LpVariable("B", 0, None, LpInteger) 
x3 = LpVariable("C", 0, None, LpInteger)

Define Objective Function

In this step, we will define the maximum objective function by adding it to the LpProblem object.

# Define Objective
model += 12 * x1 + 25 * x2 + 38 * x3 

Define the Constraints

In this step, we will add only 1 constraint defined in the problem by adding them to the LpProblem object.

# Define Constraints
model += x1 + 2*x2 + 3*x3 <= 10  # Cargo storage capacity 10 ton ; pump A is 1 ton, pump B is 2 tons and pump C is 3 ton.

Solve Model

In this step, we will solve the LP problem by calling solve() method. We can print the final value by using the following for loop.

# The problem is solved using PuLP's choice of Solver
model.solve()

# Print the variables optimized value
for v in model.variables():
    print(v.name, "=", v.varValue)
    
# The optimised objective function value is printed to the screen
print("Value of Objective Function = ", value(model.objective))

Output:
A = 1.0
B = 0.0
C = 3.0
Value of Objective Function =  126.0

Summary

In this article, we have learned about Integer Programming, Knapsack Problems, Cargo Loading Problems, Problem Formulation, and implementation in python using the PuLp library. We have solved the cargo loading problem using an integer programming problem in Python. Of course, this is just a simple case study, we can add more constraints to it and make it more complicated. In upcoming articles, we will write more on different optimization problems and its solution using Python. You can revise the basics of mathematical concepts in this article and learn about Linear Programming in this article.