Solving Assignment Problem using Linear Programming in Python
Learn how to use Python PuLP to solve Assignment problems using Linear Programming.
In earlier articles, we have seen various applications of Linear programming such as transportation, transshipment problem, Cargo Loading problem, and shift-scheduling problem. Now In this tutorial, we will focus on another model that comes under the class of linear programming model known as the Assignment problem. Its objective function is similar to transportation problems. Here we minimize the objective function time or cost of manufacturing the products by allocating one job to one machine.
If we want to solve the maximization problem assignment problem then we subtract all the elements of the matrix from the highest element in the matrix or multiply the entire matrix by –1 and continue with the procedure. For solving the assignment problem, we use the Assignment technique or Hungarian method, or Flood’s technique.
The transportation problem is a special case of the linear programming model and the assignment problem is a special case of transportation problem, therefore it is also a special case of the linear programming problem.
In this tutorial, we are going to cover the following topics:
Assignment Problem
A problem that requires pairing two sets of items given a set of paired costs or profit in such a way that the total cost of the pairings is minimized or maximized. The assignment problem is a special case of linear programming.
For example, an operation manager needs to assign four jobs to four machines. The project manager needs to assign four projects to four staff members. Similarly, the marketing manager needs to assign the 4 salespersons to 4 territories. The manager’s goal is to minimize the total time or cost.
Problem Formulation
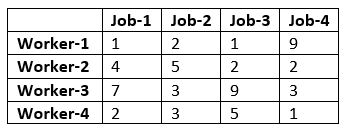
A manager has prepared a table that shows the cost of performing each of four jobs by each of four employees. The manager has stated his goal is to develop a set of job assignments that will minimize the total cost of getting all 4 jobs.
Initialize LP Model
In this step, we will import all the classes and functions of pulp module and create a Minimization LP problem using LpProblem class.
# # Import all classes of PuLP module
from pulp import *
workers=[1,2,3,4]
jobs=[1,2,3,4]
# Cost Matrix
costs=[[1,2,1,9],
[4,5,2,2],
[7,3,9,3],
[2,3,5,1]]
prob = LpProblem("Assignment Problem", LpMinimize) Define Decision Variable
In this step, we will define the decision variables. In our problem, we have two variable lists: workers and jobs. Let’s create them using LpVariable.dicts() class. LpVariable.dicts() used with Python’s list comprehension. LpVariable.dicts() will take the following four values:
- First, prefix name of what this variable represents.
- Second is the list of all the variables.
- Third is the lower bound on this variable.
- Fourth variable is the upper bound.
- Fourth is essentially the type of data (discrete or continuous). The options for the fourth parameter are
LpContinuousorLpInteger.
Let’s first create a list route for the route between warehouse and project site and create the decision variables using LpVariable.dicts() the method.
# The cost data is made into a dictionary
costs= makeDict([workers, jobs], costs, 0)
# Creates a list of tuples containing all the possible assignments
assign = [(w, j) for w in workers for j in jobs]
# A dictionary called 'Vars' is created to contain the referenced variables
vars = LpVariable.dicts("Assign", (workers, jobs), 0, None, LpBinary)Define Objective Function
In this step, we will define the minimum objective function by adding it to the LpProblem object. lpSum(vector)is used here to define multiple linear expressions. It also used list comprehension to add multiple variables.
# The objective function is added to 'prob' first
prob += (
lpSum([vars[w][j] * costs[w][j] for (w, j) in assign]),
"Sum_of_Assignment_Costs",
)Define the Constraints
Here, we are adding two types of constraints: Each job can be assigned to only one employee constraint and Each employee can be assigned to only one job. We have added the 2 constraints defined in the problem by adding them to the LpProblem object.
# There are row constraints. Each job can be assigned to only one employee.
for j in jobs:
prob+= lpSum(vars[w][j] for w in workers) == 1
# There are column constraints. Each employee can be assigned to only one job.
for w in workers:
prob+= lpSum(vars[w][j] for j in jobs) == 1Solve Model
In this step, we will solve the LP problem by calling solve() method. We can print the final value by using the following for loop.
# The problem is solved using PuLP's choice of Solver
prob.solve()
# Print the variables optimized value
for v in prob.variables():
print(v.name, "=", v.varValue)
# The optimised objective function value is printed to the screen
print("Value of Objective Function = ", value(prob.objective))Output: Assign_1_1 = 1.0 Assign_1_2 = 0.0 Assign_1_3 = 0.0 Assign_1_4 = 0.0 Assign_2_1 = 0.0 Assign_2_2 = 0.0 Assign_2_3 = 1.0 Assign_2_4 = 0.0 Assign_3_1 = 0.0 Assign_3_2 = 1.0 Assign_3_3 = 0.0 Assign_3_4 = 0.0 Assign_4_1 = 0.0 Assign_4_2 = 0.0 Assign_4_3 = 0.0 Assign_4_4 = 1.0 Value of Objective Function = 7.0
From the above results, we can infer that Worker-1 will be assigned to Job-1, Worker-2 will be assigned to job-3, Worker-3 will be assigned to Job-2, and Worker-4 will assign with job-4.
Summary
In this article, we have learned about Assignment problems, Problem Formulation, and implementation using the python PuLp library. We have solved the Assignment problem using a Linear programming problem in Python. Of course, this is just a simple case study, we can add more constraints to it and make it more complicated. You can also run other case studies on Cargo Loading problems, Staff scheduling problems. In upcoming articles, we will write more on different optimization problems such as transshipment problem, balanced diet problem. You can revise the basics of mathematical concepts in this article and learn about Linear Programming in this article.




